Sound Waves Frequency And Domain_3
Acoustics in the Frequency Domain
Introduction
Acoustics is the field of physics that models sound waves by changes in pressure. 2 approaches to model audio-visual systems are common: I approach is to model acoustics in the time domain and the other is to model in the frequency domain. This tutorial focuses on the modeling of sound in the frequency domain and makes use of the Helmholtz fractional differential equation (PDE) as the model. The acoustic modeling in the frequency domain introduced here will build on concepts introduced in the tutorial Acoustics in the Fourth dimension Domain which should exist read as a start exposure to acoustics modeling. Since the two approaches are related the relations will be presented throughout this tutorial.
The principal model of acoustics in the frequency domain is the Helmholtz equation. The Helmholtz PDE is a fourth dimension independent equation. Considering the Helmholtz PDE is a time independent PDE it can exist solved more than efficiently compared to the time dependent wave equation used for modeling acoustics in the time domain. The Helmholtz equation is, yet, just applicable when modeling acoustic systems which take a harmonic fourth dimension dependency. In other words, an inharmonic sound signals have to be modeled in the time domain, and the benefits of using the Helmholtz equation can not be exploited.
Two types of analysis in the frequency domain are introduced in this tutorial: Fourth dimension Harmonic Assay and Eigenfrequency Analysis. Both the time harmonic and the eigenfrequency assay are based on the Helmholtz PDE model in conjunction with diverse types of boundary atmospheric condition, which are also introduced in this tutorial. The purpose of a fourth dimension harmonic analysis is to compute the frequency response of an audio-visual system over a range of frequencies. An eigenfrequency analysis on the other hand is applied to solve for the eigenmodes and eigenfrequencies of an acoustic arrangement. The actual analysis of a fourth dimension harmonic model is done with ParametricNDSolve and for an eigenfrequency assay NDEigensystem is fabricated utilize of.
Extended examples of sound organization modeling tin exist found in the Model Collection.
The symbols and corresponding units used throughout this tutorial are summarized in the Classification department.
Time Harmonic Analysis
Time harmonic assay is a co-operative of acoustics concerned with the frequency response of an audio-visual organisation. A sound signal is referred to equally time-harmonic if it tin can exist expressed as a sine function with a specific frequency. For a time harmonic assay an acoustic organization is exposed to several harmonic sound signals over a range of frequencies, and the operation of the device at frequency of interest is analyzed. This blazon of analysis is important when building frequency-dependent acoustic systems, for case a low-laissez passer filter that is designed to benumb sound at higher frequencies.
In response to harmonic stimulus the resulting audio pressure level field 
can be shown to be time-harmonic as well [1]. A sound pressure field is said to exist time-harmonic if the pressure variation at any spatial position 
has a sinusoidal fourth dimension dependence with an angular frequency 
.
A full general expression of a harmonic audio pressure field 
is written as:
Here 
denotes the amplitude at the given position, and 
is an initial phase shift at 
. In cases where two sound signals take no stage difference 
are said to exist "in phase". If the stage deviation happens to be 
, the two sound signals are said to be "in antiphase".
For analytical convenience, the time-harmonic relation (two) is often expressed in circuitous class known as the complex exponential representation (CER):
Past convention the CER expression is often expressed only as:
in which it is implicitly interpreted that the real part of the circuitous expression represents the real function 
.
The CER expression can be understood as a rotating vector 
in the complex plane. The following figure illustrates this behavior.
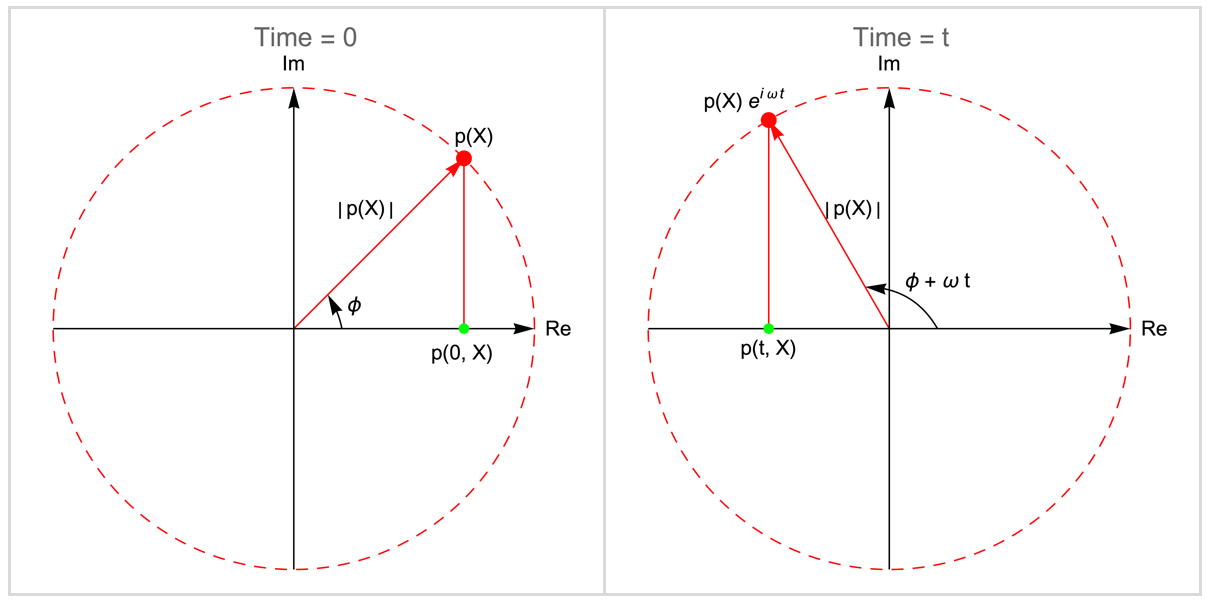
The rotating vector 
is known equally the complex amplitude office. The amplitude office 
rotates counterclockwise at a speed of the angular frequency 
. At any given time 
the project of 
on the real axis represents the transient sound pressure 
, and the vector length 
corresponds to the local aamplitude.
If we limited the amplitude function and its circuitous conjugate as 
and 
, then the local amplitude 
tin exist calculated by:
When the time harmonic relation (3) is inserted into the wave equation the equation simplifies to a time contained Helmholtz equation. The derivation of the Helmholtz equation from a moving ridge equation volition be presented in a later department entitled Derivation of the frequency acoustic model from time domain model. For now it is of import to understand that an unknown sound field can be solved for in the frequency domain past using the angular frequency 
in the Helmholtz PDE model (four):
The terms 
and 
are monopole and dipole sources, respectively.
The computed solution 
, however, tin be hands transformed back into time domain using the time-harmonic relation (5).
Eigenfrequency Assay
If the monopole source 
and the dipole source 
are removed from the Helmholtz PDE model (6), the equation simplifies to the source-free Helmholtz equation:
Equation (seven) tin can be treated as an eigenvalue problem such that 
, and can be solved with NDEigensystem. Here the differential operator 
corresponds to the left hand side of (8), and 
represents the eigenvalue of the eigensystem.
The set of eigenvalues 
that fulfills the source-gratuitous Helmholtz equation gives the corresponding eigenfrequencies 
by:
or
The aamplitude role 
that is paired with each eigenvalue 
is chosen eigenmode.
The eigenfrequency 
is also known equally the natural frequency, which determines the resonance of an acoustic organisation. To illustrate the acoustic resonance we consider an open-ended tube and a airtight-concluded tube. Both tubes are filled with air, and the length 
.
Past convention, the closed-ended tube denotes a tube with one closed cease only.
Since the medium pressure must be equal to the ambient reference force per unit area at the open end, the sound pressure is stock-still at cipher such that 
. At the closed end, however, the sound force per unit area accumulates and reaches its maximum value since no forward motion is possible. Due to these boundary conditions the tube tin simply sustain sound waves at certain frequencies, that is, the eigenfrequencies.
At each eigenfrequency 
a standing moving ridge forms within the tube. The lowest eigenfrequency, which corresponds to eigenmode 1, is chosen the fundamental frequency. As shown in the acoustics time domain tutorial, compared to a traveling moving ridge with the aforementioned amplitude a continuing wave needs a weaker sound source. In other words, a sound source excites an acoustic system the most at each eigenfrequency.
Eigenfrequency assay is therefore an important consideration when designing acoustic systems that utilize (or foreclose) resonance, such as musical instruments, acoustic filters and concert halls.
Helmholtz Equation
Introduction to Helmholtz Equation
The behaviour of an acoustics system in the frequency domain is investigated by repetitively solving the Helmholtz PDE for a specific frequency out of a frequency range of involvement. The Helmholtz equation (nine) is used for modeling a harmonic sound force per unit area field at a specific angular frequency 
:
The dependent variable in the Helmholtz equation is the sound pressure level 
. The sound pressure moving ridge is propagating in a medium with density 
at the speed of sound 
. The sound pressure field is modeled in response to a harmonic audio stimulus at a frequency 
, which is related to the angular frequency 
by 
.
Audio pressure can be understood every bit the local pressure level departure from an ambient reference pressure: 
, where 
denotes the position vector. Terms 
and 
represent monopole and dipole sources, respectively. The Source Types department describes these audio sources.
Various sections in the documentation explain the utilise of inactive PDE operators. Please refer to Numerical Solution of Partial Differential Equations.
As shown in the tutorial Acoustics in the Time Domain, the transient audio-visual model can be set up in a similar manner:
Notation that for the frequency domain acoustic model, the time derivative term 
has been converted to the frequency dependent term 
by using the time-harmonic relation (10). The derivation tin can be found in the following section: Derivation of the frequency audio-visual model from time domain model.
The post-obit model parameters are used for the examples in this tutorial. These parameters ascertain the simulation domain 
.
The following 1D example shows a frequency domain acoustic model simulation. In the first step a time harmonic analysis will be performed and in the subsequent pace an eigensystem analysis is washed of the aforementioned acoustic mode. The relation between the two analysis types will and then be apparent.
In a next footstep an eigenvalue analysis is performed.
.
and the frequency response spectrum. Note that at each eigenfrequency 
the amplitude response 
reaches its local maximum.
Derivation of the frequency acoustics model from the time domain model
The Helmholtz equation is derived from the wave equation (11) with harmonic time-dependence. The general moving ridge equation is given every bit:
Here the terms 
and 
are monopole and dipole sources, respectively.
Recall that if a sound pressure level field is causeless to be fourth dimension-harmonic, the pressure level variation in time for a particular frequency 
tin be expressed in the complex airplane by an amplitude function 
:
Likewise, the monopole and dipole sources can be expressed by amplitude functions 
and 
, respectively:
Taking the second social club time derivative of (12) gives:
Taking the slope of (thirteen) yields:
Insert (xiv), (fifteen), (16) into (17), the wave equation becomes:
Gene out the mutual term 
then the equation simplifies to the fourth dimension-independent, inhomogeneous Helmholtz equation (xviii):
Model Parameter Setup
In acoustics simulations the wavelength 
of a sound wave needs to exist resolved past a sufficiently fine mesh in club to get an authentic numerical solution of the governing partial differential equation. Here nosotros create a function to prepare the MaxCellMeasure for time harmonic waves.
For a time harmonic wave the wavelength is 
. The default resolution of the max edge length is set to 12 nodes per 
, which ways that there volition exist at least twelve elements per wavelength 
in each direction of the wave propagation. Typically this is sufficient to resolve waves accurately [19]. However, it is ever possible to assign other resolution values to meet different accuracy requirements.
In many examples we volition be using a radiation purlieus condition to produce a harmonic sound wave, and an absorbing boundary condition to avoid moving ridge reflection.
Source Types
The Helmholtz PDE model (twenty) contains 2 types of time harmonic sources: monopole 
and dipole sources 
. The post-obit sections will demonstrate how these audio sources are gear up for modeling in the frequency domain. The physical meaning of audio sources is explained in particular in the acoustics time domain tutorial.
Monopole Sources
The monopole source 
from the Helmholtz equation (21) models a point source that radiates sound isotropically. An instance of an acoustic monopole would be a minor sphere whose radius alternately expands and contracts [22].
To make use of a monopole source nosotros accept to specify the monopole source forcefulness 
and the source location 
. The monopole source term 
may be written as:
where 
is a regularized Dirac delta office at the source location.
There are diverse techniques to regularize the delta function [23,24]. In this tutorial we choose:
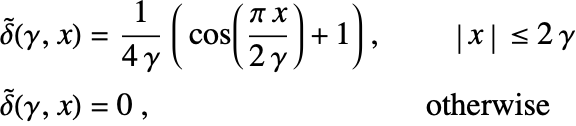
where 
is the regularization parameter that controls the back up of the regularized delta functions 
. Typically 
should have a size comparable to the mesh spacing 
.
As shown in the section entitled Time Harmonic Assay, the solution from the Helmholtz PDE is the circuitous valued amplitude role 
, which contains the information of both phase and amplitude. The amplitude of the audio pressure corresponds to the accented value or circuitous modulus 
.
.In a 1D domain the sound pressure level amplitude 
is constant for the monopole source 
at each detail frequency. Inside the source region 
there is a small deviation in 
due to the discrete nature of the regularized delta function 
used. A effectively mesh tin exist used to reduce the numerical mistake.
Note that for a given monopole source forcefulness 
, the pressure amplitude reduces with higher frequencies. The analytical solution [25] for the amplitude in 1-dimension is given past:
It is more intuitive to consider the sound pressure 
every bit a office of fourth dimension. To do so the amplitude part 
should be transformed via the harmonic wave relation (26): 
.
The monopole source is a point source that radiates sound isotropically at 
. The blue line hither is the transient audio force per unit area 
, and the gray line is the analytical pressure aamplitude inserted for a visual verification.
As a comparing, a second monopole source is constructed in a like manner.
.For 2D and 3D monopoles, equally the radiated sound moving ridge spreads out from the source a wider wavefront volition be formed. Therefore, with a given monopole strength 
the pressure level amplitude 
will decrease with the distance to the source location.
Dipole Sources
A dipole source 
consists of two monopole sources of equal strength but opposite phase and separated by a distance 
. The separation distance is small compared to the wavelength of sound 
. An example of an acoustic dipole would be a small rigid sphere that oscillates sinusoidally [27]. Dissimilar a single monopole source 
, a dipole source does non radiate audio isotropically.
In the acoustics time domain tutorial it has been shown that a dipole source 
could be modeled by two identical monopole sources 
. Hither we direct jump to model a dipole source with the source term 
.
To make use of a dipole source we have to specify the dipole source strength 
and the source location 
. The dipole source term 
may be written as:
where 
is the regularized delta function at the source location.
Every bit shown in the section entitled Time Harmonic Analysis, the solution from the Helmholtz PDE is the complex valued amplitude function 
, which contains the information of both stage and amplitude. The amplitude of the sound force per unit area corresponds to the accented value or complex modulus 
.
.In 1D domain the audio pressure amplitude 
is constant exterior each dipole source region. Since the embedded monopole sources are in opposite phase, the amplitude at the source location 
sums up to zero. The analytical solution [28] for the pressure amplitude in 1D is given by:
The numerical solution plot above, however, is slightly different from the analytical solution due to the discrete nature of the regularized delta function 
used. A finer mesh can be used to reduce the numerical error.
Information technology is more intuitive to consider the sound pressure 
as a function of fourth dimension. To do then the amplitude office 
should exist transformed via the harmonic moving ridge relation (29): 
.
The dipole source does not radiate sound isotropically. The resultant sound waves are sinusoidal but in opposite phase.
Equally a comparison, a 2d dipole source is constructed in a similar style.
.For 2D and 3D dipoles the radiated sound moving ridge does not spread out equally in all directions [30]. Therefore, with a given dipole strength 
the pressure level amplitude 
volition depend on both the spatial direction and the altitude to the source location.
Sound Propagation in Lossy Media
As shown in the acoustics time domain tutorial, it is possible to model sound propagation in lossy media with a given porosity 
, menstruation resistivity 
and an constructive bulk modulus 
. The modified moving ridge equation is:
Inserting the harmonic moving ridge relation 
and factoring out the common term 
, the equation (31) becomes:
Equation (32) is the modified Helmholtz equation that is used to model sound attenuation in the frequency domain.
The effective majority modulus 
is frequency-dependent [33], and can be approximated past an empirical formula:
To illustrate the lossy media model nosotros consider a sound moving ridge propagating through a tube filled with a porous absorber. The porosity and flow resistivity of this material are given by 
and 
, respectively.
. An absorbing boundary condition is added on the right to avert a reflection of the wave. Notation that the NeumannValue is set to 
[34] to conform for the modified Helmholtz equation (35).
is added on the left end using DirichletCondition.Since the effective bulk modulus 
in (36) is a frequency-dependent variable, the attenuation charge per unit of the amplitude 
also varies with different frequencies. The small wiggles near the right end result from the numerical reflection on the absorbing boundary, and tin be reduced by using a effectively mesh.
The amplitude of the sound pressure wave decays every bit information technology propagates to the right. Note that the attenuation rate slightly varies with different frequencies.
A Comparison of Time Domain and Frequency Domain Modeling
An acoustic arrangement can be modeled both in the time domain and the frequency domain. As shown in the acoustics time domain tutorial, the wave equation is used to notice a transient solution of a sound moving ridge in the time domain. Whenever the excitation of a sound pressure field is time-harmonic, the Helmholtz equation can be used to straight solve for a steady-state solution of a sound force per unit area field in the frequency domain. Each approach has its ain strength and constraints, and is summarized in the following table.
| Fourth dimension Domain Modeling | Frequency Domain Modeling | |
| Governing PDE | Wave equation | Helmholtz equation |
| Dependent variable | transient p (t,X) | stationary p (Ten) |
| Harmonic excitation | yes | yes |
| Inharmonic excitation | yes | no |
| Computational toll | high | low |
| Accuracy | depression | loftier |
In other words, if an acoustic organization has a time inharmonic dependency then it needs to be modeled in the fourth dimension domain, and the benefits of using the Helmholtz equation tin can not be exploited. But in all other cases making use of the model in the frequency domain is beneficial.
To illustrate this behaviour an audio-visual organization of a right-traveling wave is considered in the side by side example. The simulation is washed once in the time domain, and in one case in the frequency domain. In both models the simulation domain is ready as four times of the wavelength 
, and the frequency is arbitrarily chosen at 
.
In the post-obit example a radiations boundary condition is added on the left to produce a harmonic sound moving ridge, and an arresting boundary condition is placed on the right to avoid wave reflection.
First nosotros volition analyse the model in the fourth dimension domain, and following that a frequency domain assay will be performed. The results will be compared to each other.
Wave Equation: Time Domain Modeling
For the wave equation model, the simulation end time 
is defined as the fourth dimension required for the sound pressure field to attain its dynamic steady state.
The issue shows a transient sound pressure level wave traveling to the right.
Next, we build the same model with the Helmholtz equation.
Helmholtz Equation: Frequency Domain Modeling
Note, that the setup of the equation does not change. All changes are done through changing the variables and parameters.
Since the Helmholtz equation directly computes a stationary solution of a sound pressure field, there is no need to do the time integration in the solving procedure. The computational price is thus reduced significantly.
The result of the Helmholtz equation is a steady-state sound pressure field 
. To transform the solution into the time domain the harmonic wave relation can be used:
To transform a transient solution into the frequency domain, withal, requires a Fourier Analysis [37]. The procedure is to decompose the transient audio signal into a sum of harmonic signals. Each harmonic betoken has a specific frequency and a relative magnitude, which allows the states to map the transient signal into the frequency domain.
The computational price for solving the Helmholtz equation is so much lower that it is possible to solve the Helmholtz PDE repetitively with different frequencies, which makes it suitable for frequency domain modeling.
Next, nosotros compare the accurateness of the wave equation model and the Helmholtz equation model.
Accuracy Comparison
Since the wave equation model is a time-dependent PDE while the Helmholtz equation model is not, the former is subject to an extra error from the numerical time integration. The Helmholtz model is therefore more than accurate than the wave equation model.
Acoustic Boundary Atmospheric condition
In the acoustics time domain tutorial, we have shown the details of mutual audio-visual boundary conditions and how they can be modeled in the time domain. To avoid the repetition the following section only describes how to build these boundary weather condition in the frequency domain. For readers who are interested in the derivation and the physical explanation, please refer to the acoustics time domain tutorial.
Almost common boundary conditions in acoustics can be modeled with DirichletCondition, NeumannValue and PeriodicBoundaryCondition, and can exist categorized in the post-obit four types:
- Robin Type
- Neumann Type
- Dirichlet Type
- Periodic Type
Generally speaking, in solver algorithms a NeumannValue[ k-q p(X) , 10∈ Γ b ] is used to specify the flux over the boundary 
such that 
holds.
Even so, in acoustic models the dipole sources 
tin can only be specified within the domain and will ever equal to zero on any function of the purlieus and leads to 
.
For each boundary status we volition land whether the particular boundary condition is applicable for Fourth dimension Harmonic Analysis or Eigenfrequency Analysis or both in the following manner:
Impedance Boundary Weather condition
Conception
With a specified impedance 
on the boundary 
, the impedance boundary condition is given past:
modeled with NeumannValue.Derivation
When a audio moving ridge transits to another medium or encounters a partially reflective boundary, for example a porous surface, part of the audio moving ridge will be reflected at the interface and role will exist transmitted across the interface.
One property that is used to formulate the relation between the incident, reflected and transmitted wave is called the specific acoustic impedance. The specific acoustic impedance 
is the ratio of the sound pressure to the sound particle velocity as the wave moves through the medium, which is defined as:
From the acoustics time domain tutorial we know that the impedance purlieus condition tin can exist formulated with a given purlieus impedance 
as:
Inserting the harmonic moving ridge relation 
and factoring out the mutual term 
, and so the impedance boundary status can be applied in the frequency domain every bit:
Here the wave number 
denotes the ratio of angular frequency to the speed of sound.
An impedance purlieus condition tin can be used with:
Impedance Purlieus Conditions in Fourth dimension Harmonic Assay
To illustrate the impedance boundary condition a tube with a porous surface at the right end is considered in the next example. The porous surface is treated every bit an impedance boundary since information technology is a partially cogitating boundary.
.
.It is more intuitive to inspect the sound moving ridge in the time domain. Recall that the solution can be transformed back into time domain with the harmonic wave relation (38): 
.
Since the impedance boundary models a partially cogitating boundary, at that place is more than free energy moving to the right than at that place is being reflected, which makes the resulting wave appear to travel to the correct. Annotation that the maximum and the minimum values of the pressure amplitude are fixed in infinite (dashed lines). This type of moving ridge is chosen a partial continuing wave.
The ratio between the maximum and the minimum amplitudes is known as the standing wave ratio (SWR):
.The standing moving ridge ratio (SWR) is shown to be independent of the frequency. For an unknown boundary the SWR can be used to measure the impedance 
and the reflection coefficient 
given the specific acoustic impedance, 
, of the domain:
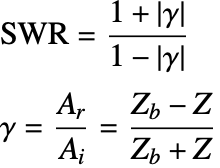
Here 
and 
are the amplitude of the reflected and the incident wave, respectively.
Absorbing Purlieus Conditions
Formulation
With a specific type of incident wave and the altitude 
between the wave origin to the purlieus 
, the absorbing purlieus status is given by:
- Airplane moving ridge:
- Cylindrical moving ridge:
- Spherical wave:
modeled with NeumannValue.Derivation
Typically a simulation domain that extends to infinity is not a feasible option in a simulation. Absorbing boundary atmospheric condition are a methodology used to model infinite domains. An arresting purlieus condition (ABC) works past absorbing an incoming wave and thus makes the model behave as if information technology had space extent. ABC are not the simply manner to model simulation domains with infinite extent. Perfectly Matched Layers (PML) may be used equally an alternative approach to an ABC.
From the time domain tutorial we know that the absorbing boundary condition is given by:
and inserting the harmonic wave relation 
gives the absorbing boundary status in the frequency domain.
Note that for a aeroplane wave 
, for a cylindrical wave 
and for a spherical wave 
are used.
An absorbing boundary condition can be used with:
Absorbing Boundary Conditions in Fourth dimension Harmonic Analysis
Equally an example we look at an infinitely long tube with the computational domain set from 
to 
. To model the continuation of the domain nosotros add together a plane wave absorbing boundary status at the correct cease.
.Since the resulting audio pressure field is simply a right-traveling harmonic wave, the pressure amplitude is fixed at 
throughout the domain for all frequencies.
The incoming wave is absorbed at the right hand boundary as if the simulation domain had infinite extent.
Sound Hard Boundary Conditions - Walls
Conception
For a wall purlieus 
, the sound hard boundary condition is given by:
modeled with NeumannValue.Derivation
On a audio hard boundary, the normal component of the audio particle velocity 
is nil since no forrad motion is possible:
Substituting (39) into the momentum conservation equation 
and applying the harmonic moving ridge relation (40) 
, then the sound difficult purlieus condition can be formulated in the frequency domain as:
If no boundary condition is specified on whatever function of the boundary so past default a Neumann zero purlieus condition is implicitly used. This implies that a sound hard purlieus is the default purlieus condition used if no boundary condition is specified at a given boundary.
A audio hard boundary status can be used with:
Sound Hard Purlieus Weather in Time Harmonic Analysis
Equally an example for a time harmonic analysis, we look at a tube with i end airtight.
.The shape of the amplitude field shows several minima and maxima points, which are known as "nodes" and "antinodes", respectively. In the time domain nodes are positions where the standing wave has no displacement and antinodes are the positions with maximal displacement. In the frequency domain the displacement manifest themselves as minima and maxima. Since no forward move is possible on the sound hard boundary, the audio pressure 
is fixed at its maximum at the right end, which means it is ane of the antinodes. The maximum value 
corresponds to the double of the aamplitude set by the radiations boundary.
It is more intuitive to audit the event in the time domain.
Note that the sound wave neither moves right nor left only simply oscillates in fourth dimension. This type of moving ridge is known as a standing moving ridge, which is formed by the superposition of ii waves traveling in contrary directions.
In this case the right-traveling wave is produced past the radiation purlieus and the left-traveling wave is the reflected wave from the audio hard boundary. For readers who are interested in the way that travelling waves superimpose to give a standing wave, please refer to the acoustics time domain tutorial.
Sound Hard Purlieus Conditions in Eigenfrequency Analysis
Unlike a fourth dimension harmonic analysis, an eigenfrequency analysis aims to find the eigenfrequencies 
and the corresponding eigenmodes (eigenfunctions) of an audio-visual system. In the next example nosotros consider a tube with both end closed.
.Annotation that the first eigenfrequency is zero, corresponding to the solution without any sound. The offset pair of eigenfrequency/eigenmode is therefore a trivial solution, and is denoted as eigenmode 0.
As explained previously, the audio pressure is fixed at its maximum on the audio hard boundaries since no forward movement is possible.
Normal Velocity Boundary Conditions
Formulation
With a specified sound particle velocity 
on the boundary 
, the normal velocity boundary condition is given by:
.Derivation
When a nonzero, time harmonic sound particle velocity is specified at a boundary, then this type of boundary is called a normal velocity boundary:
Substituting (41) into the momentum conservation equation 
and applying the harmonic wave relation (42) 
, then the normal velocity boundary status tin exist formulated in the frequency domain every bit:
A normal velocity boundary status can be used with:
Normal Velocity Boundary Atmospheric condition in Fourth dimension Harmonic Analysis
In the following instance a harmonic vibration is introduced at the right hand purlieus and vibrates with a known velocity amplitude 
. The sound field tin can be calculated past using NeumannValue as shown below.
.Since the resulting wave is simply a left-traveling harmonic wave, the amplitude distribution is fixed throughout the domain for all frequencies.
The normal velocity purlieus generates a harmonic wave on the right end that propagates to the left.
As shown in the acoustics time domain tutorial, a normal velocity boundary could be replaced by a force per unit area source boundary when the specific acoustic impedance 
is known.
Sound Soft Boundary Conditions
Formulation
The sound soft purlieus condition is given by:
modeled with DirichletCondition.Derivation
On a sound soft boundary the medium pressure is fix equal to an ambient reference pressure, which means that the sound pressure at the boundary is stock-still at naught: 
:
A sound soft boundary condition can be used with:
Sound Soft Purlieus Weather condition in Fourth dimension Harmonic Assay
As an case for the time harmonic analysis, we look at a tube with one end open. The open-concluded side is treated every bit a sound soft boundary since there is no constraint to limit the audio moving ridge movement.
.With 
the sound pressure is a minimum at 
, where a sound soft boundary is positioned, and is thus called a node. The maximum value of the audio pressure field corresponds to the double of the amplitude fix by the radiations boundary.
Similar as the sound hard boundary, the resulting wave is a standing wave that is formed by the superposition of 2 waves traveling in reverse directions.
In this example the right-traveling wave is produced past the radiations boundary and the left-traveling wave is the reflected wave from the sound soft purlieus. For readers who are interested in the style that travelling waves superimpose to give a standing moving ridge, please refer to the acoustics fourth dimension domain tutorial.
Sound Soft Purlieus Conditions in Eigenfrequency Assay
To illustrate the behavior of sound soft boundaries in an eigenfrequency assay, we consider a tube with both ends open.
.As expected, the sound pressure level on the audio soft boundaries is fixed at zero.
Pressure level Source Purlieus Weather
Conception
With a specified pressure level aamplitude 
on the purlieus 
, the pressure source boundary condition is given by:
modeled with DirichletCondition.
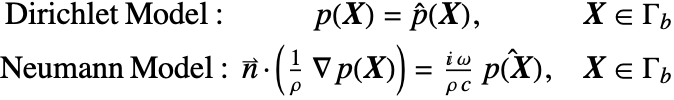
modeled with NeumannValue.Derivation
Nosotros speak of a pressure level source boundary status when a nonzero, fourth dimension harmonic sound pressure is specified at a purlieus. Both DirichletCondition and NeumannValue can be used to specify a pressure source boundary condition:
A pressure level source boundary status can be used with:
Pressure level Source Boundary Conditions in Fourth dimension Harmonic Assay
Dirichlet Model
To formulate the Dirichlet condition of a pressure source boundary, we simply rewrite equation (43) with the harmonic wave relation (44) 
:
Here 
denotes the amplitude of the pressure source.
.Since the resulting wave is simply a left-traveling harmonic wave, the amplitude distribution is fixed at 
throughout the domain.
Similar to the normal velocity purlieus, the pressure level source generates a harmonic wave on the right end that propagates to the left.
Neumann Model
A pressure source can also be modeled with a NeumannValue. As shown in the acoustics time domain tutorial the NeumannValue setting for a pressure source is given past:
Insert the harmonic wave relation (45) 
, then the pressure source boundary condition can be formulated in the frequency domain every bit:
.The animation shows the aforementioned outcome as the Dirichlet model. For readers who are interested in the trade-off between the Neumann model and the Dirichlet model of a pressure source purlieus, please refer to the corresponding department in the acoustics time domain tutorial.
Radiation Boundary Atmospheric condition
Formulation
With a specified incident sound force per unit area 
and a wave direction vector 
on the boundary 
, the radiation purlieus status is given by:
The relation between the boundary normal vector 
, the wave direction vector 
and the wave incident angle 
is illustrated below:
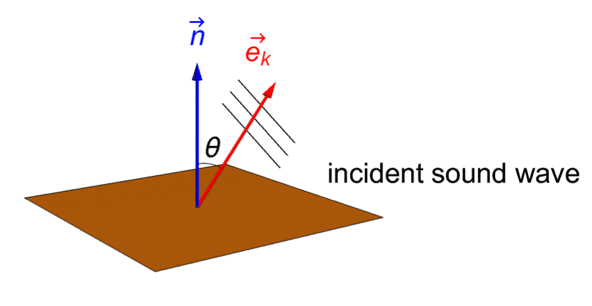
Therefore, equation (46) can likewise exist expressed with a moving ridge incident angle 
as
modeled with NeumannValue.Note that when applying a radiations boundary in the 1D domain the incident angle 
is e'er zero (i.e. normal incidence) and the equation (47) simplifies to:
A 1D radiation boundary instance will be shown in the following department. A 2nd instance, which demonstrated a radiated sound wave with oblique incidence, is presented here.
Derivation
A radiation boundary is a hybrid boundary status that combines the properties of a pressure level source purlieus and an arresting boundary. A time harmonic sound pressure 
is specified at a boundary to produce an incoming moving ridge, however, unlike a simple pressure source the radiations boundary allows an approachable wave to leave the computational domain with little reflection.
As shown in the acoustics time domain tutorial the radiation boundary condition is given by:
Insert the harmonic moving ridge relation (48) 
, then the radiation purlieus status can be formulated in the frequency domain as:
A radiation purlieus condition tin can exist used with:
Radiation Purlieus Conditions in Fourth dimension Harmonic Analysis
As an case a semi-infinite tube with ane terminate closed is considered in the adjacent instance. The correct end is treated as a radiation purlieus where the harmonic sound wave enters the computational domain, and the airtight left end is set as a audio difficult boundary.
.The resulting audio pressure field shows a standing moving ridge, which is formed past the superposition of both incoming and outgoing waves. In this case the radiations boundary at 
generates an incoming left-traveling moving ridge, and the implicit sound difficult boundary at 
reflects the moving ridge to the right every bit an outgoing wave, which leaves the domain from the radiation boundary without constrained. For readers who are interested in the fashion that travelling waves superimpose to give a standing wave, please refer to the acoustics time domain tutorial.
Floquet Periodic Boundary Atmospheric condition
Formulation
Given a function 
that maps the sound pressure 
from the source purlieus 
to the periodic boundary 
, the Floquet periodic boundary condition can exist written as:
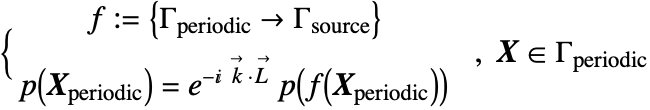
Here 
is the showtime altitude from the periodic boundary 
to the source boundary 
, and 
is the wave number vector that denotes the management of the audio wave.
Derivation
A Floquet periodic boundary condition is used to model a time harmonic acoustic moving ridge within a spatially periodic domain. That is, the information obtained from one boundary, referred to as the source boundary 
, can exist mapped to some other boundary, referred as the periodic purlieus 
, with a mapping function 
. The Floquet periodic purlieus status is fix upward with a PeriodicBoundaryCondition in the audio-visual PDE model.
A Floquet periodic purlieus condition can be used with:
Floquet Periodic Boundary Weather condition in Time Harmonic Analysis
Equally an instance consider the following periodic construction in the 
plane. The structure is assumed to extend to infinity forth 
and 
directions. With the usage of the periodic boundary condition it is possible truncate the structure and take the unit of measurement jail cell equally the simulation domain 
.
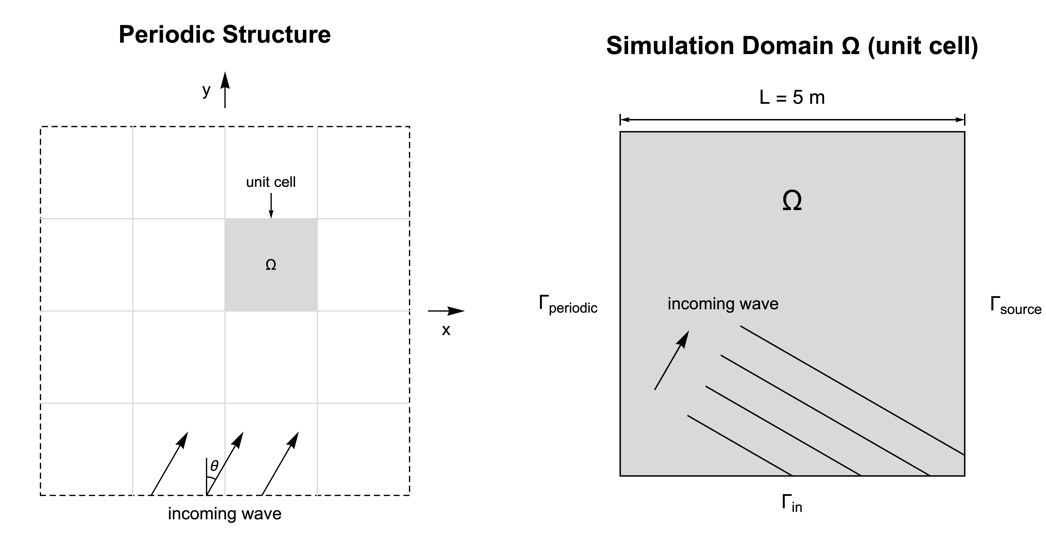
In this model an acoustic wave is coming from the bottom edge with an incident angle 
, and is modeled with a 2nd radiations purlieus denoted as 
. Nosotros set the periodic boundary 
on the left edge and the source boundary 
on the correct edge, and so that when the sound moving ridge pass through the correct side of the domain 
it reappears on the left side with the same magnitude.
Furthermore, nosotros need to simulate the approachable wave though the boundaries. In this case an arresting boundary status is not applicable due to the non-normal outbound angle. An alternative technique called "perfectly matched layer (PML)" is used instead. Further details on PML can be constitute in the following section entitled perfectly matched layers (PML).
To implement a PML the simulation domain is extended to include a PML region:
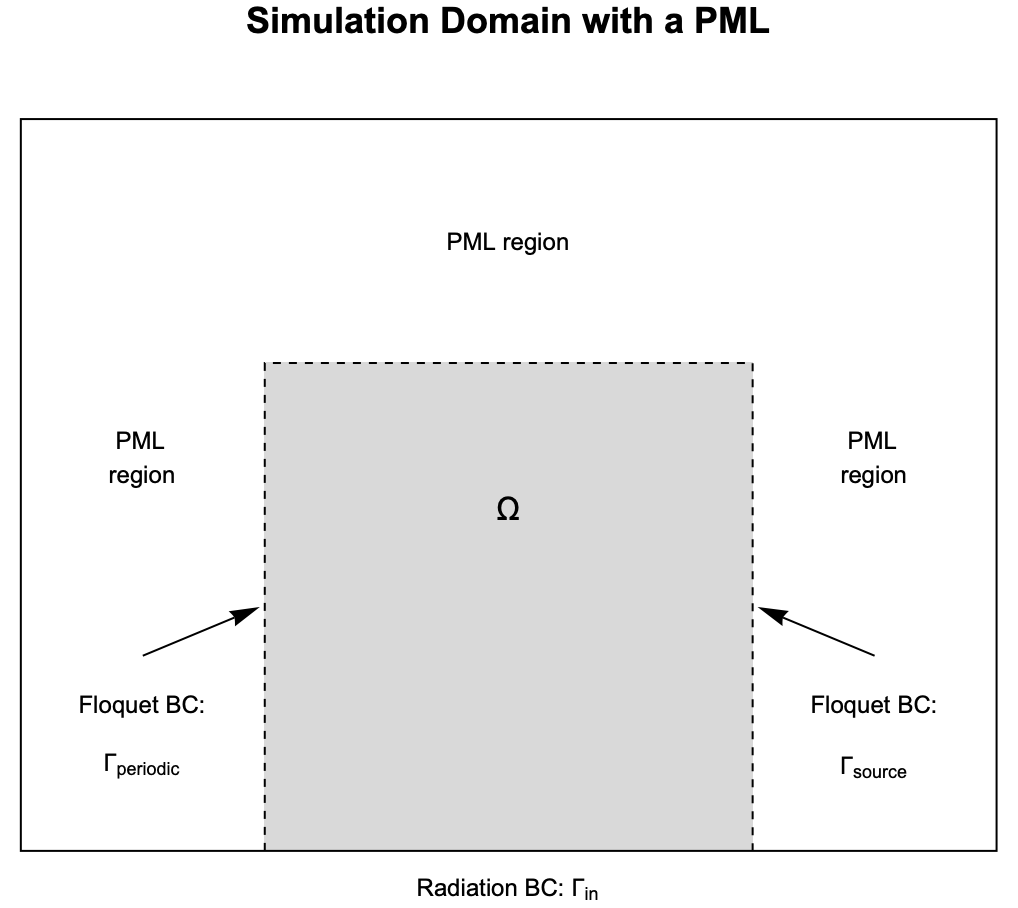
To set up the 2D domain that preserves the internal boundary between the regular domain 
and the PML region, we need to generate the mesh manually. A detailed explanation nigh the mesh generation tin can exist plant in the Chemical element Mesh Generation tutorial.
In club to get a adept issue with PML implemented, a finer than the default grid is used for the mesh generation. Hither we set the max edge length to be 
, which means that there will be at least ten elements in the 
(length) and 
(width) directions of the domain 
.
from equation (49).Side by side nosotros set up the Floquet periodic boundary condition on the left edge. Note that the start distance between the periodic purlieus 
(left edge) and the source boundary 
(right edge) is 
.
and the corresponding mapping function.
.To simulate the entering sound wave with an oblique incidence, a 2nd radiations purlieus condition is applied on the lesser edge of the domain.
.Meet this note nigh improving the visual quality of the animation.
The blitheness shows a non-normal audio wave propagating over the domain. As the moving ridge pass through the correct boundary it re-appears on the left side due to the spatial periodicity. Since the sound medium is assumed to be acoustic lossless, the magnitude of the moving ridge remains at a constant level at all times.
Perfectly Matched Layer (PML)
A perfectly matched layer (PML) is a method to model simulation domains with space extent. As such a PML is an alternative method to absorbing boundary condition. The post-obit section shows how to implement a PML for a Helmholtz PDE used in frequency domain modeling. The full derivation and the caption can be found in the appendix section of the acoustics time domain tutorial.
To implement a PML two things demand to happen. First the simulation domain needs to be enlarged. This extension is the region in which the PML is active. Second, a coordinate transformation of the PDE is washed.
The iii dimensional Helmholtz equation after the PML coordinate transformation [50] is given in by:
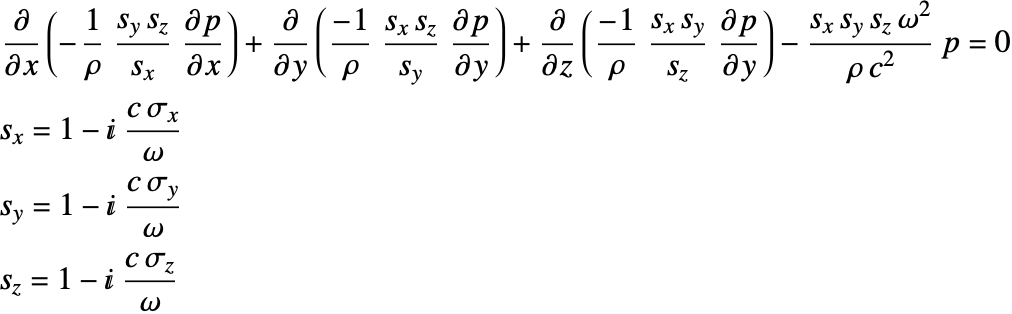
Here 
, 
and 
are the absorbing coefficients of the PML. Three auxiliary variables 
, 
and 
are introduced to control the PML attenuation in each dimension.
In the 1D case where 
, the equation (51) simplifies to:
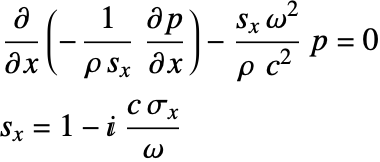
The absorption coefficient 
is a tuning parameter to be chosen, and is gear up to increase linearly within the PML layer from 
to 
. A thinner PML requires a greater value of 
but large 
tends to increment numerical reflections.
The perfectly matched layer can be used with:
.Perfectly Matched Layer in Fourth dimension Harmonic Analysis
Equally an example we consider a simulation of a 1D domain from 
to 
using a computational domain that ranges from 
to 
with a PML at the right from 
to 
.
.Equally seen 
in the original non-PML region.
.The sound force per unit area in the non-PML region is fixed at the incident amplitude 
, so decays to zero within the PML region. To minimize the numerical reflection at the PML interface, the absorption coefficient 
and the PML width should exist chosen carefully. The tradeoff between these two parameters is discussed in the acoustics time domain tutorial.
The wave is attenuated within the PML but remains unchanged in the original domain, and the attenuation rate is contained of frequencies.
Nomenclature
| Symbol | Description | Unit of measurement |
| ρ | density of a medium | [kg/mthree] |
| c | speed of audio in a medium | [m/s] |
| p | sound pressure | [Pa] |
| p | local sound aamplitude | [Pa] |
 | specified boundary pressure | [Pa] |
 | conjugate of sound pressure level | [Pa] |
| t | time | [south] |
| t end | simulation terminate time | [s] |
| Ten | position vector | [one thousand] |
| due south | management switch | Northward/A |
| F | optional dipole source | [N/mthree] |
 | dipole source strength | [N/grand3] |
| θ | dipole directivity angle | [rad] |
| Q | optional monopole source | [ane/due south2] |
 | monopole source strength | [i/due southtwo] |
| d | seperation altitude of dipole source | [thou] |
| λ | wavelength of audio | [m] |
| Ω | simulation domain | [1000] |
| m | wave number | [rad/yard] |
| f | sound wave frequency | [Hz] |
| ω | sound wave angular frequency | [rad/s] |
| δ | Dirac delta function | N/A |
 | regularized delta function | Northward/A |
| γ | regularization parameter | [k] |
| h | mesh spacing | [yard] |
| X southward | audio source location | [g] |
| κ | effective bulk modulus | [Pa] |
| α | attenuation factor | [mtwo/(southward·N)] |
| ϕ | porosity | Northward/A |
| V 5 | viod book | [m3] |
| V T | full volume | [grand3] |
| R f | menses resistivity | [kg/(mthree ·s)] |
| β | standard deviation of a Gussian pulse | [m] |
| ζ | sound particle displacement | [m] |
| 5 | sound particle velocity | [thousand/southward] |
 | specified boundary velocity | [chiliad/s] |
| T | audio moving ridge period | [t] |
| Z | feature impedence | [Pa·due south/m] |
| Z b | purlieus impedance | [Pa·southward/m] |
| A r | amplitude of reflected wave | [Pa] |
| A i | amplitude of incident wave | [Pa] |
| σ | absorbtion coefficient of PML | [rad/(s·1000)] |
| σ max | maximum value of absorbtion coefficeint | [rad/(s·chiliad)] |
References
1.Ihlenburg, Frank. The Medium-Frequency Range in Computational Acoustics: Practical and Numerical Aspects. Journal of Computational Acoustics, Vol.11, No. 2 175-193, 2003.
two.Heutschi, Kurt. Lecture Notes on Acoustics I. Swiss Federal Constitute of Technology Zurich, 2016.
3.Johnson, Steven. Notes on Perfectly Matched Layers (PMLs). MIT, 2010.
four.Bilbao, Stefan and Hamilton, Brian. Directional Source Modeling In Wave-Based Room Acoustics Simulation. IEEE, 2017.
5.Peskin, Charles. The Immersed Boundary Method. Cambridge University, 2002.
6.Russell, Daniel, Titlow, Joseph and Bemmen, Ya-Juan. Acoustic monopoles, dipoles and quadropoles: An experiment revisited. American Journal of Physics 67, 660, 1999.
7.Vita, Micro. The Wave Equation with a Source. Oklahoma State University.
eight.J. De Moerloose and M. A. Stuchly, Behavior of Berenger'south ABC for evanescent waves, IEEE Microwave and Guided Wave Letters, vol. 5, no. 10, pp. 344-346, Oct. 1995.
ix.J. Berenger, Evanescent waves in PML's: origin of the numerical reflection in wave-construction interaction bug, IEEE Transactions on Antennas and Propagation, vol. 47, no. 10, pp. 1497-1503, Oct. 1999.
ten.J. De Moerloose, Jan & Stuchly, Maria. Reflection assay of PML ABCs for low-frequency applications, IEEE Microwave and Guided Wave Letters, vol. 6., no. 4, pp. 177-179, Apr. 1996.
eleven.East. Turkel and A. Yefet. Absorbing PML boundary layers for moving ridge-similar equations, Applied Numerical Mathematics, vol. 27, pp. 533-557, 1998.
12.G. Pan, A. Abubakar and T. Habashy. An constructive perfectly matched layer blueprint for audio-visual fourth-order frequency-domain finite-deviation scheme, Geophysical Periodical International, vol. 188, pp. 211-222, 2012.
13.T. J. Cox, P. D'Antonio. Acoustic absorbers and diffusers: Theory, design, and application, London: Spon Press, 2004.
fourteen.E. Westward. Weisstein. Fast Fourier Transform, MathWorld--A Wolfram Spider web Resource. Retrieve from: http://mathworld.wolfram.com/FastFourierTransform.html.
Sound Waves Frequency And Domain_3,
Source: https://reference.wolfram.com/language/PDEModels/tutorial/Acoustics/AcousticsFrequencyDomain.html
Posted by: hamptonacantiming.blogspot.com
0 Response to "Sound Waves Frequency And Domain_3"
Post a Comment